Deep Representation Learning

of Spectroscopic Graphs
  • Kelvin Lee,
  • Christine Li,
  • Brett McGuire,
  • Kyle Crabtree

ISMS 2021—Talk FF09

Scaling up molecular spectroscopy

High-resolution, high bandwidth data

Unknown molecule discovery

 Maximum information extraction from single spectra with machine learning

Potential benefits from machine learning

Unified encodings

Data compression

Mixture separation

$J, K_a, \lambda, F, \omega, +$

$A,B,C \rightarrow \nu, I$
Applying deep neural networks to analyze/generate molecular spectra

Automating spectroscopic analysis

Machine learning as an attractive method for data processing;

Models are only as good as how the data is represented!

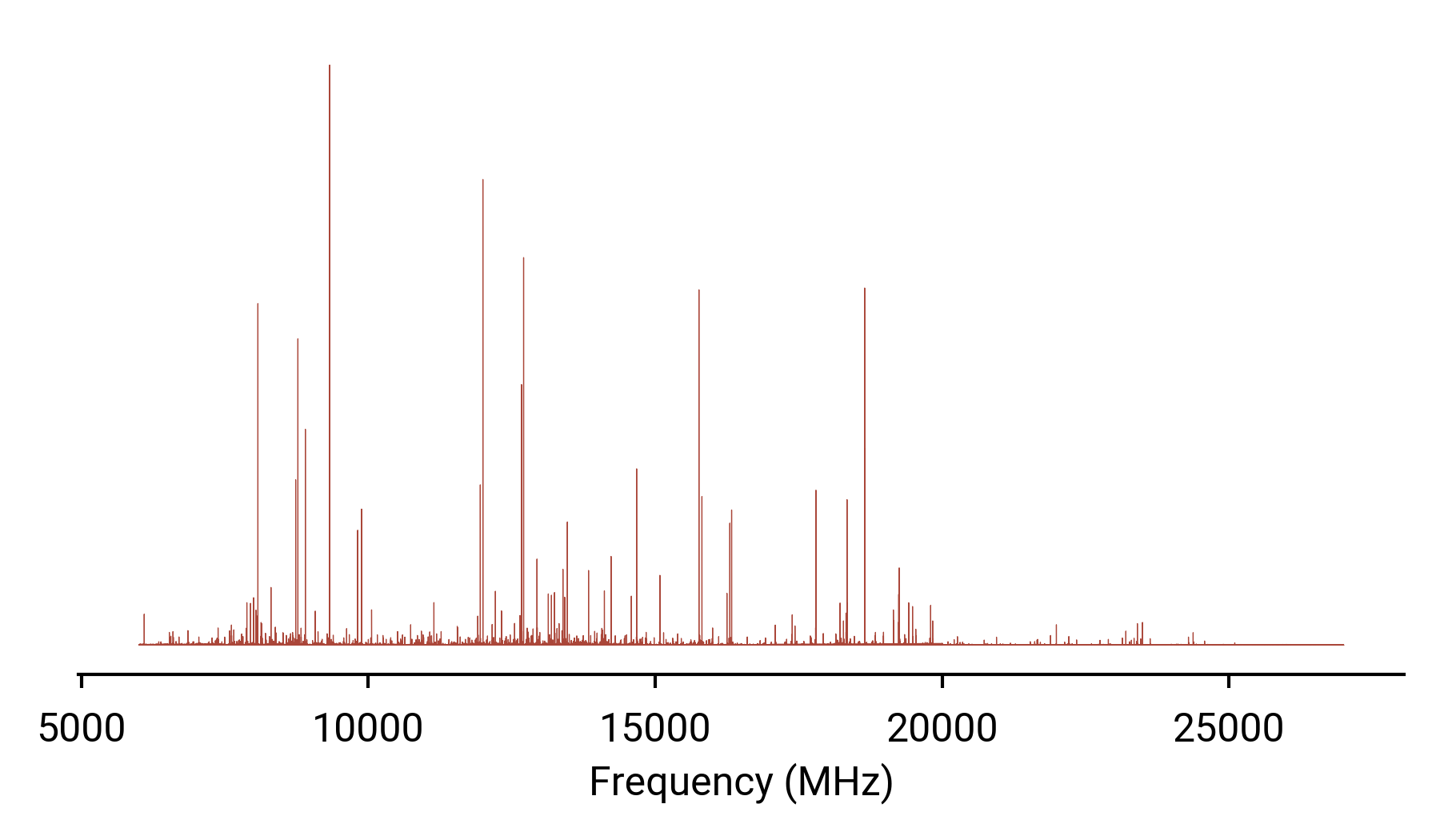
Frequency vs. intensity may be intuitive for humans, but not for machines.

  • Ordering and scale
  • Missing data
  • Computational scaling
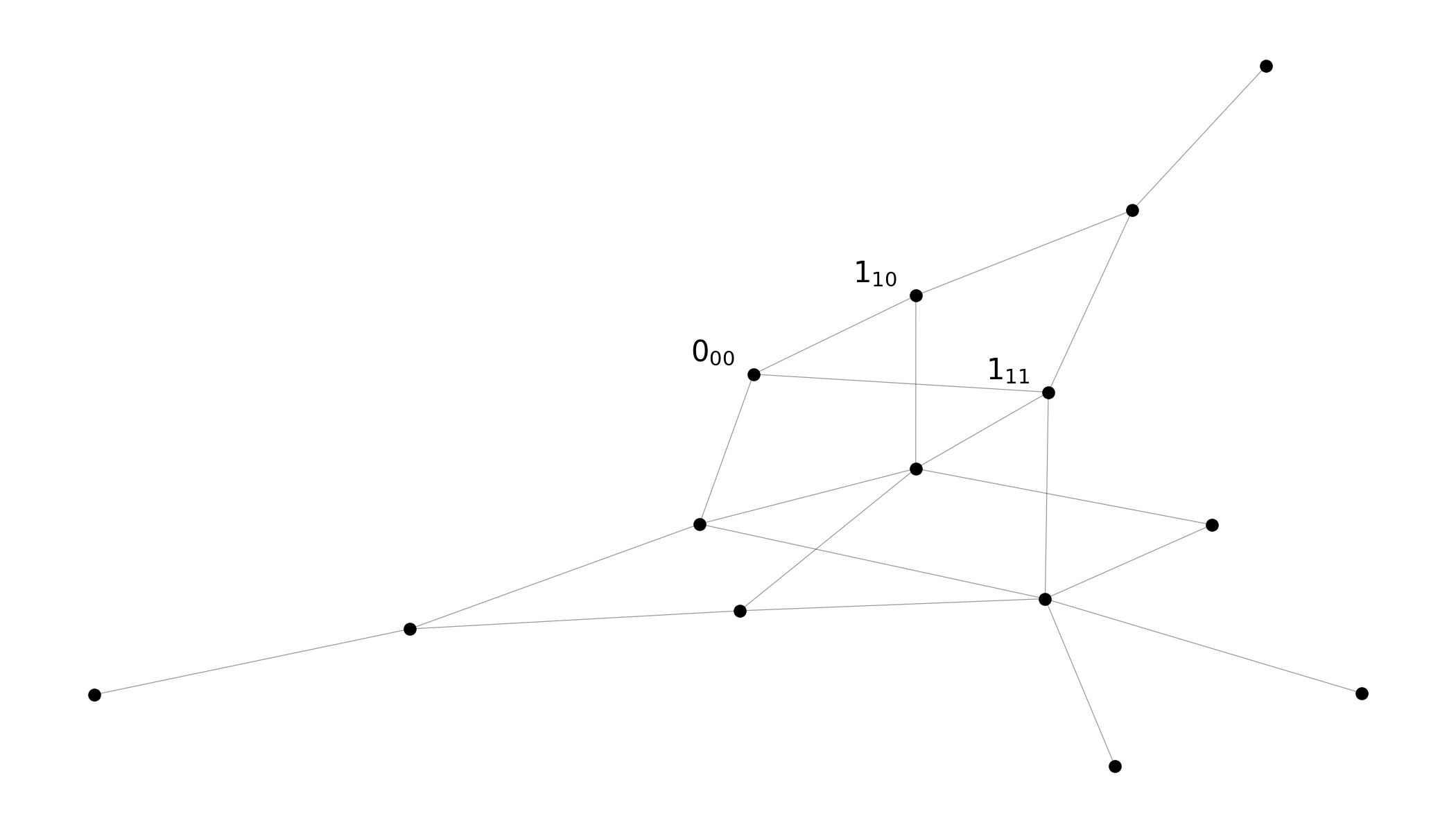
Graphs are an efficient alternative!

Spectroscopic graphs

Energy nodes connected through transition nodes

Spectroscopic graphs

Energy nodes connected through transition edges

Graph neural networks

Symmetry properties

Non-uniformity

Inductive bias

 Permutation invariance Ungriddable data Generalizable models

Learning on multiple scales: from local neighborhoods to graphs

Open questions

What can we/models learn from graph representations? Can we reconstruct spectroscopic graphs from limited information?

Data generation

10,000 rigid rotor spectra from SPCAT

Uniform sampling in $\kappa$ with scale invariant $A,B,C$

$E, J, K_a, K_c$ embedded per node

Can process 230 graphs per second on Nvidia 3070

83,000 nodes, ~330,000 edges per batch (32 full graphs)
Model trained on subgraphs to extract local information and generalize to graphs

Node learning

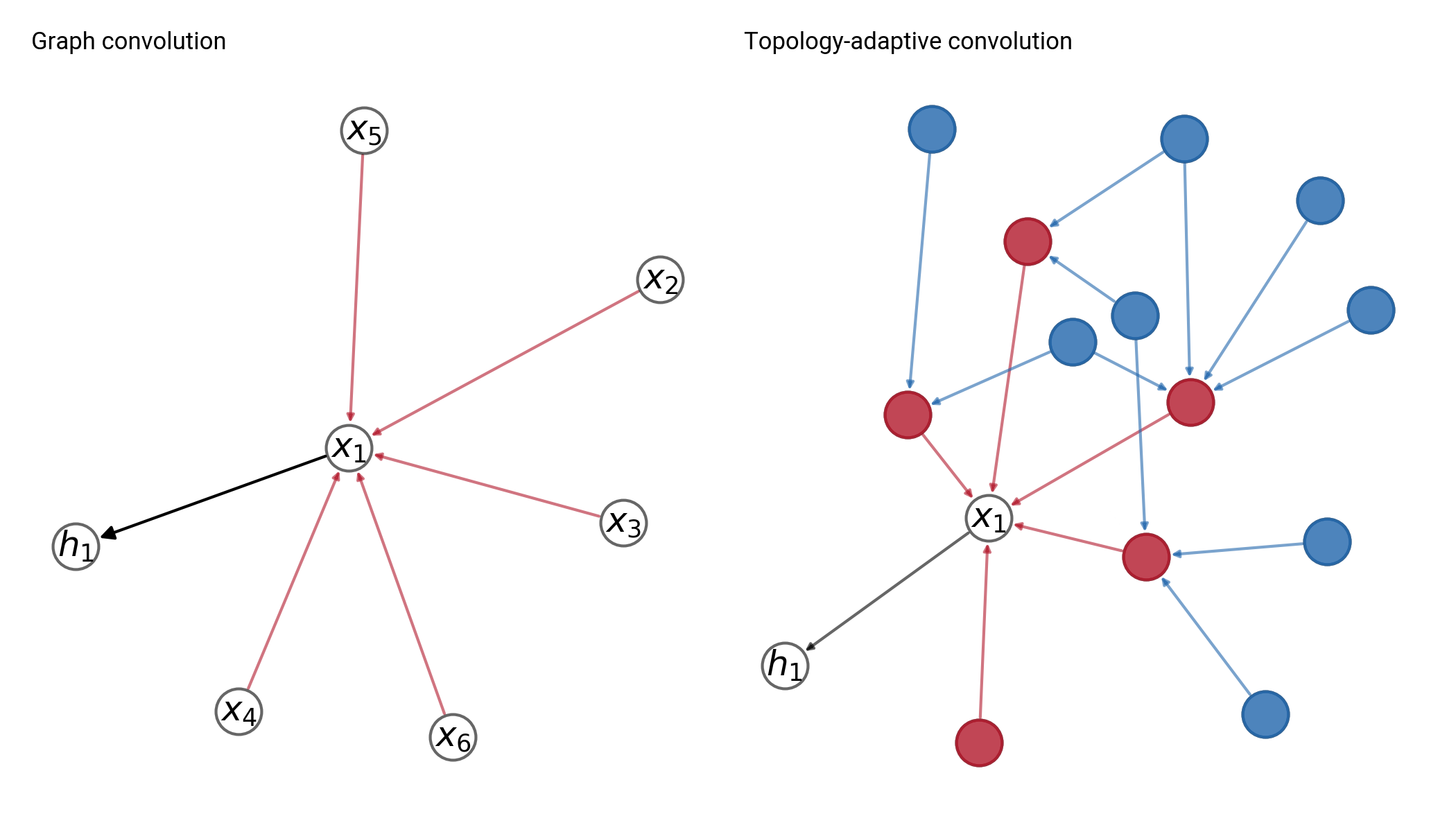
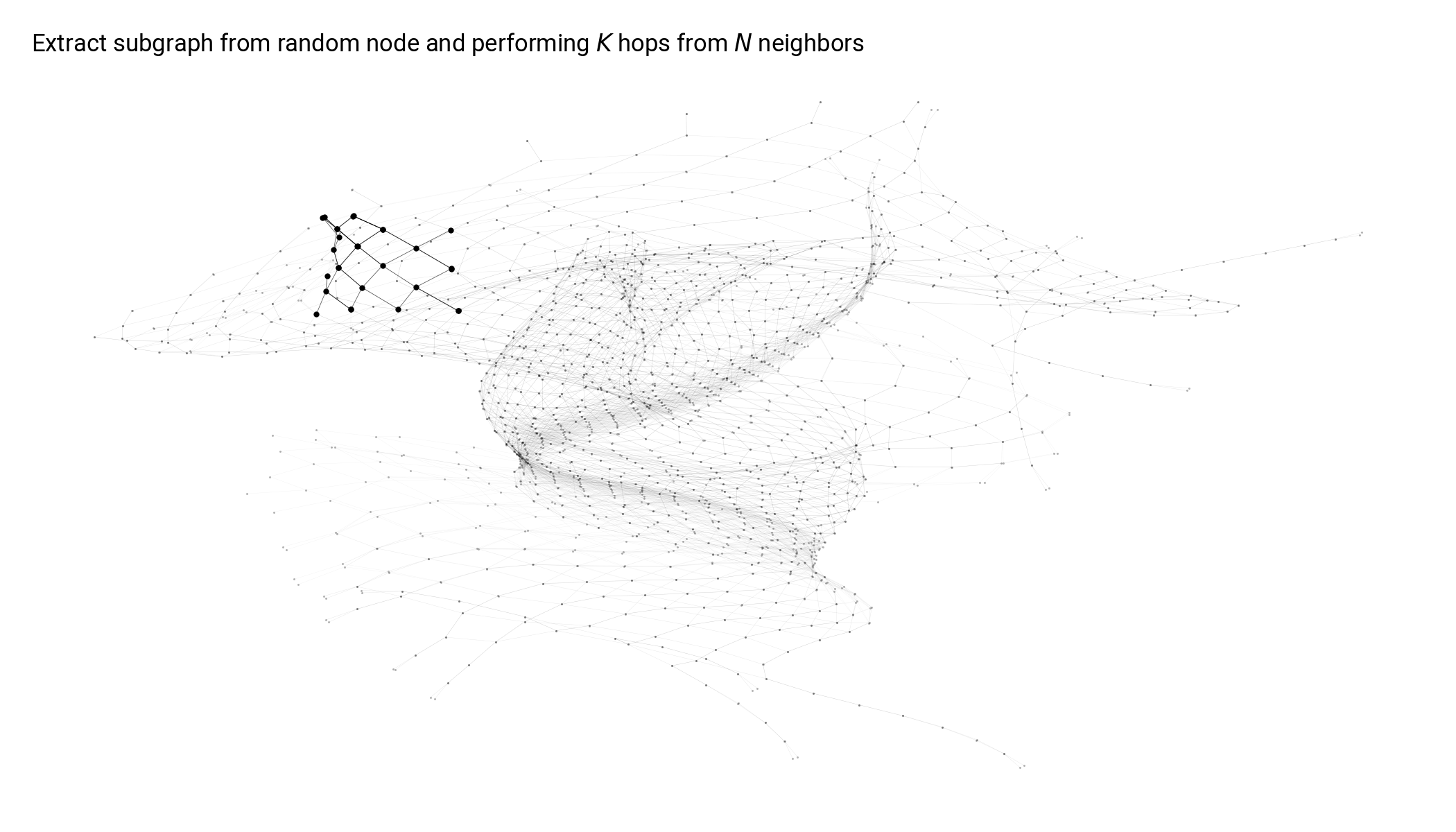
Aggregates information from up to K neighbors per node

Graph learning

Collective information for entire graphs used to predict spectroscopic parameters

$\rightarrow A, B, C$

Graph autoencoder

graph LR Graph-->Subgraph Subgraph-->Convolution Convolution-->Embedding Embedding-->AdjacencyMatrix Embedding-->Pooling Pooling-->RotationalConstants

Self-supervised representations

What do graph neural networks learn from spectroscopic graphs?

Analyzing learned node/graph embeddings

Use Uniform Manifold Approximation and Projection (UMAP)

Topology preserving 2D projection of high dimensional embeddings
https://pair-code.github.io/understanding-umap/

What to look for

Local patterns
  • Clustering of similar nodes
  • Connectivity

Large scale patterns
  • Relative locations of clusters

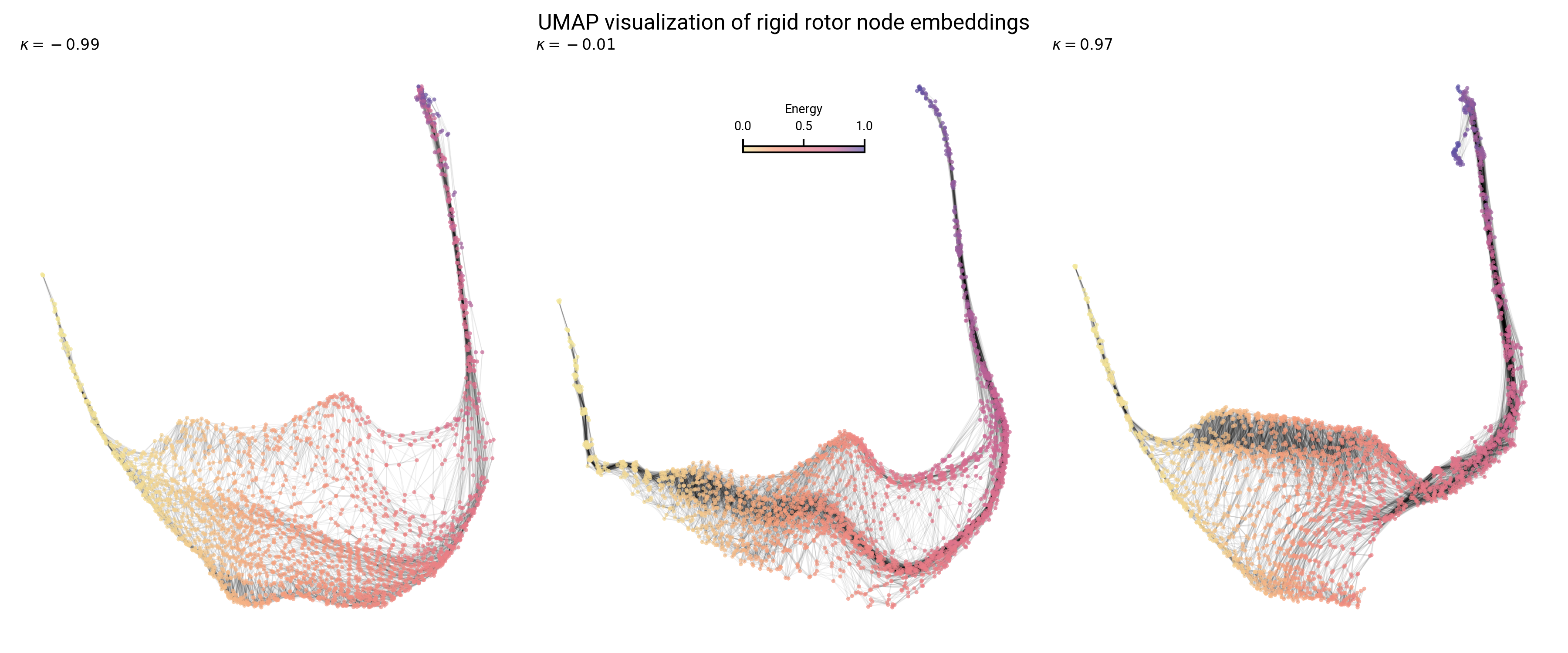
Analysis of prolate, oblate, and asymmetric top topology

Graph layout differs with asymmetry: sparsity and boundaries

Topology of node embeddings contain energy information

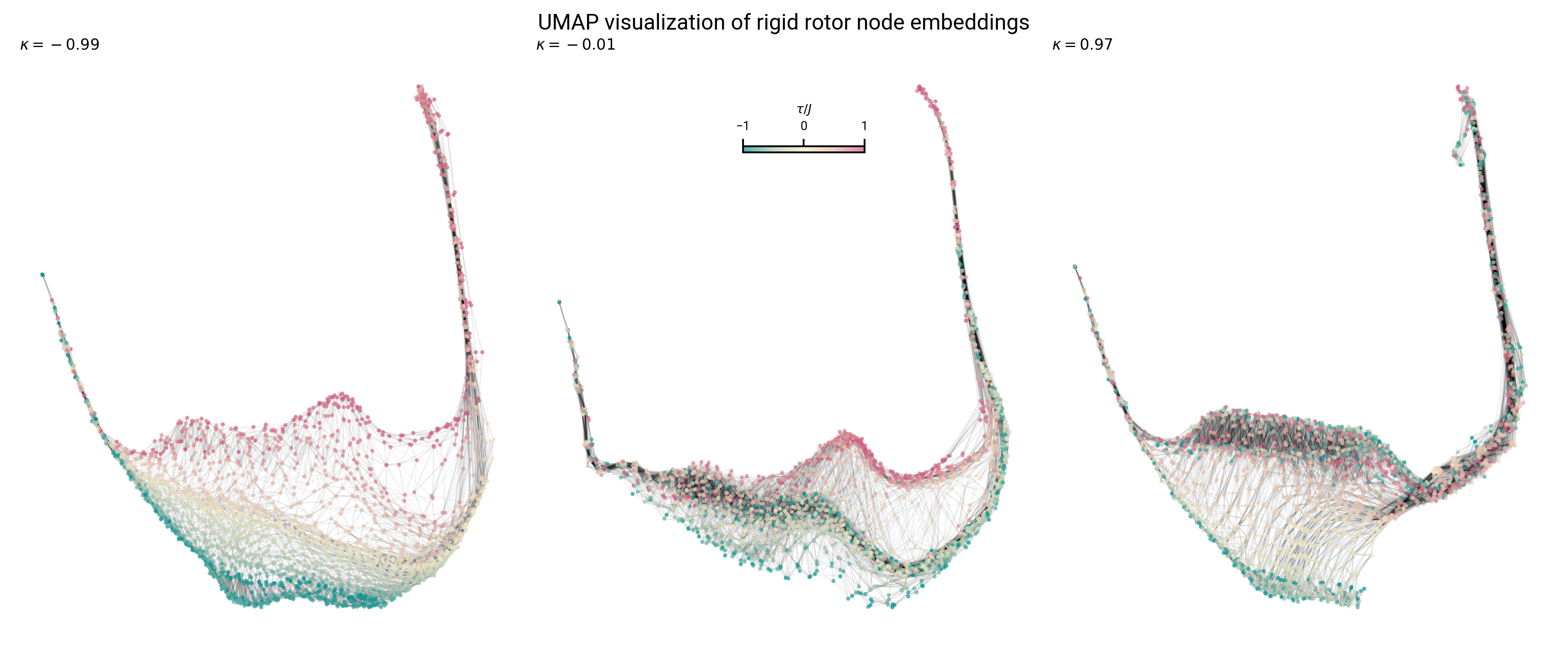
Topology of node embeddings contain quantum number information

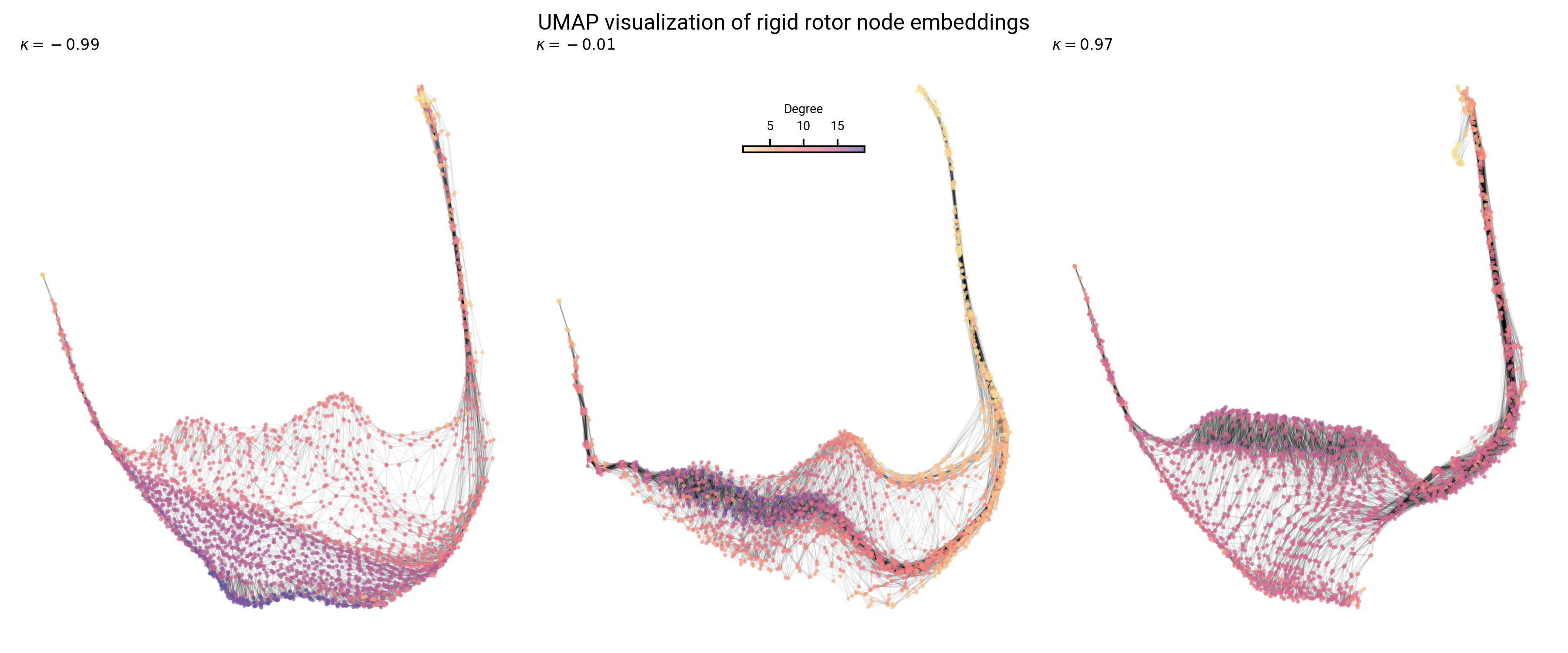
Topology of node embeddings contain neighborhood information

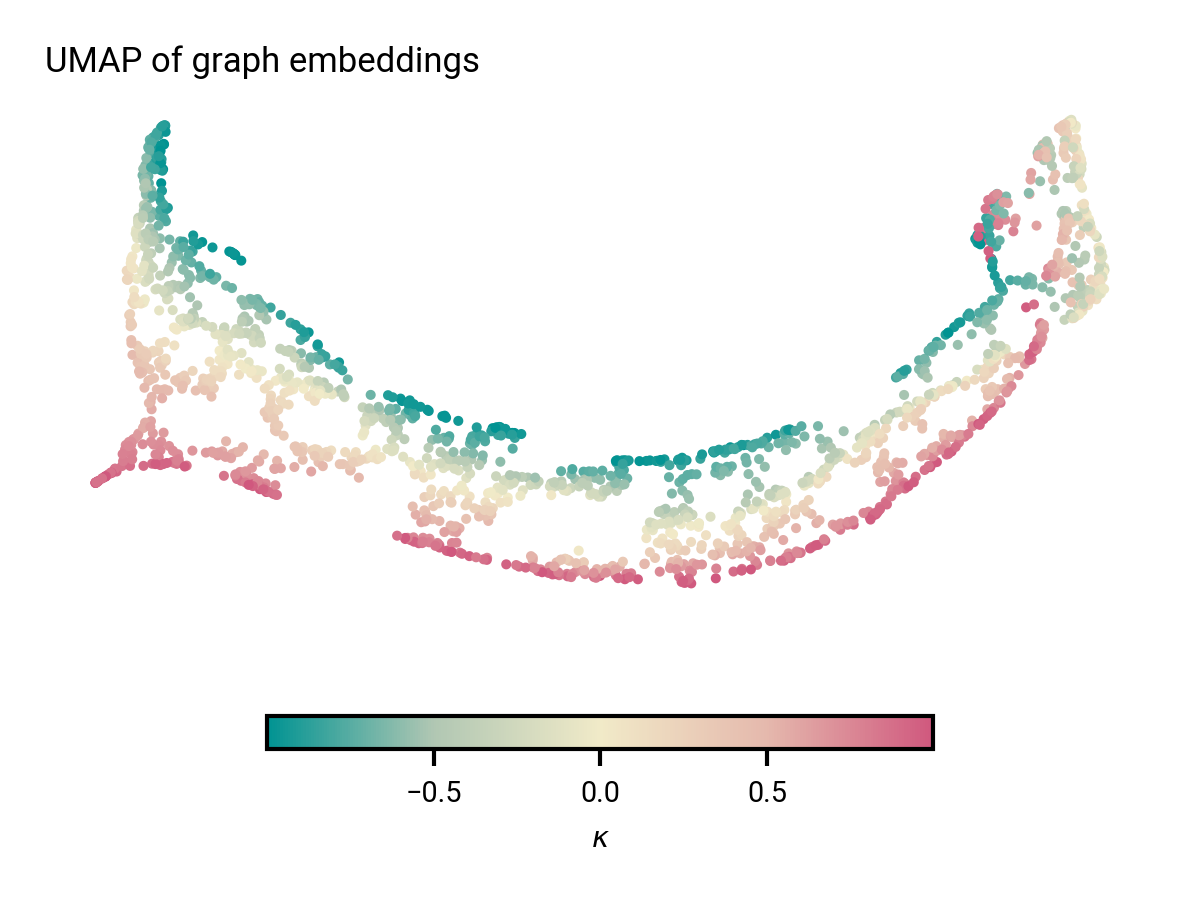
2000 graphs from validation set

Graph embeddings contain asymmetry information

Reconstructed graphs

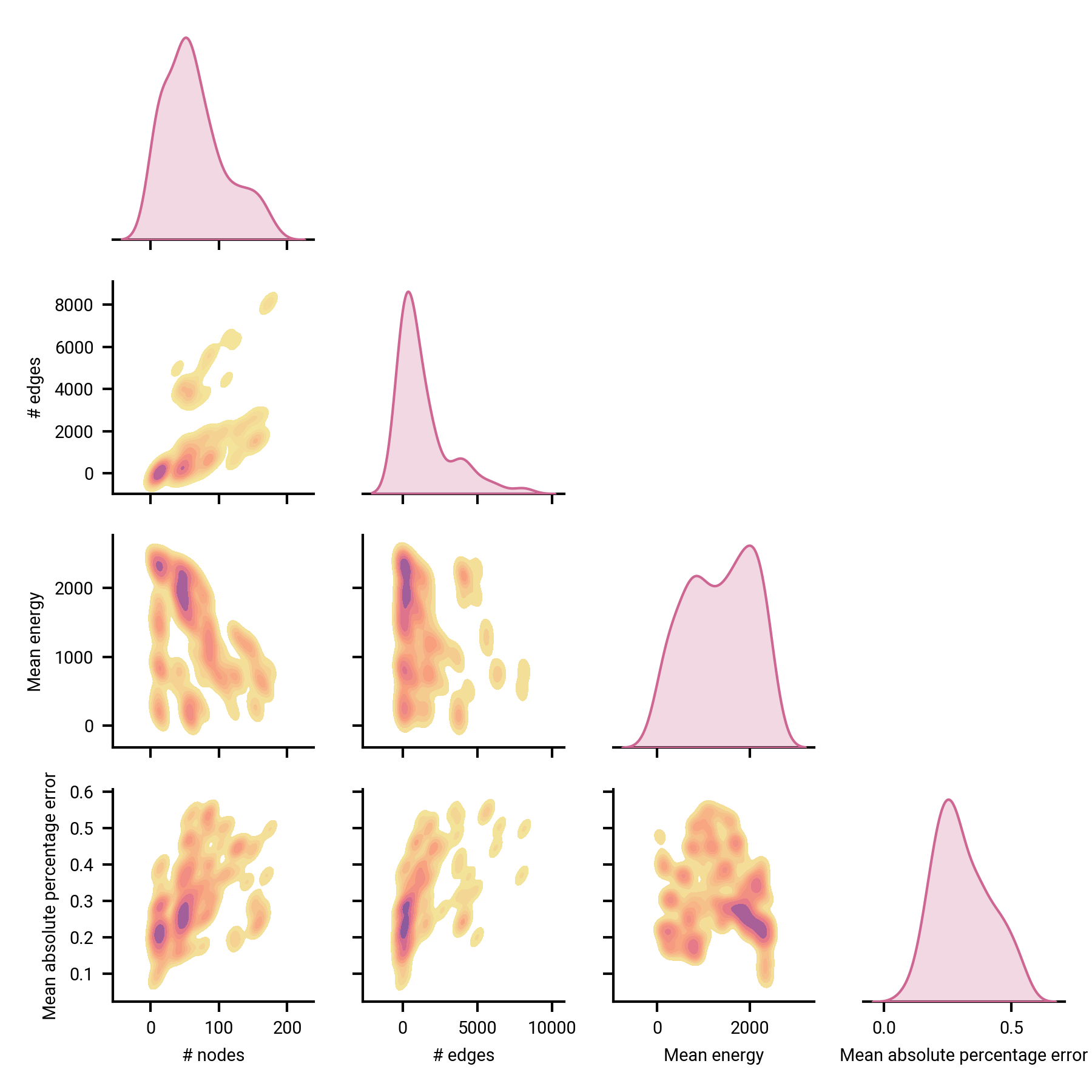
How accurate/precise are the models in reproducing spectroscopic parameters and linkage?

Dependent variables for spectroscopic parameter estimation

  • Typical accuracy ~20% for $B, C$
  • Correlated with # nodes/edges
  • Invariant to energy scale

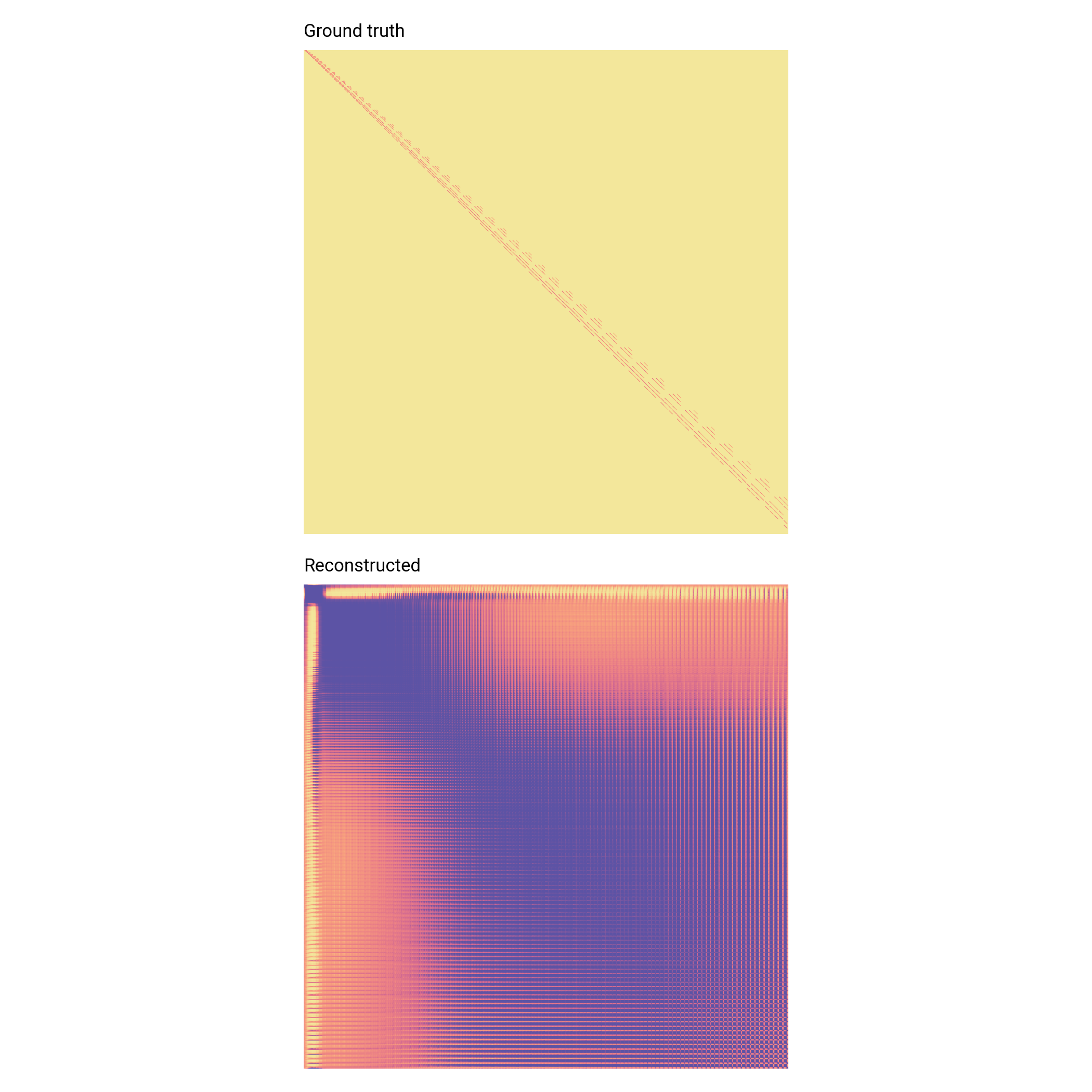
Link prediction

Simple A/B testing indicates >95% ROC AUC score (i.e. correct linkage prediction 95% of the time)

Energy levels are incredibly sparse—not the true error!

Need to improve on edge training sample scheme

Conclusions

Applying graph principles toward automating spectral analysis

Graph neural networks able to learn information-rich node and graph embeddings

Linkage prediction is far from accurate—need to revise training strategy

Acknowledgements

Thank you!

github.com/laserkelvin

@cmmmsubmm

Google scholar

Applying machine learning to molecular spectra

Use graph representations of rotational spectra

Graph/node embeddings successfully capture spectroscopic intuition