vicreg: Variance-invariance-covariance regularization for self-supervised learning

arxiv

First written: Sep/03/2021, 09:20:52

Summary

• Un/self-supervised learning of representations is difficult: embeddings can likely end up with highly correlated features¹
  • We also want to preserve the idea that similar inputs should result in similar encodings, with the most straightforward result being the same embedding regardless of inputs (i.e. a collapse). This also involves some clustering heuristic that might not be simple.
• Conventionally, good embeddings can be obtained through [[contrastive-learning]], forcing dissimilar inputs to have different embeddings, and vice versa
  • Contrastive learning is expensive, however, because to do it well you have to find examples and counterexamples during training; e.g. [[triplet-loss]] variants.
• VICReg encodes three heuristics as a form of regularization: variance, invariance, and covariance

Useful embeddings

• The requirements typically are:
  • Similar inputs -> similar embeddings (i.e. clustering)
  • Dissimilar inputs -> dissimilar embeddings (i.e. contrast)

VIC regularization

...the architecture is completely symmetric and consists of an encoder $f_\theta$ that outputs the final representations, followed by a project $h_\phi$ that maps the representations into projections in a embedding space where the loss function will be computed.

• Projector gets rid of low-level information in the representations, and is only used for computing the loss (i.e. not used for actual tasks)

Notation

Architecture

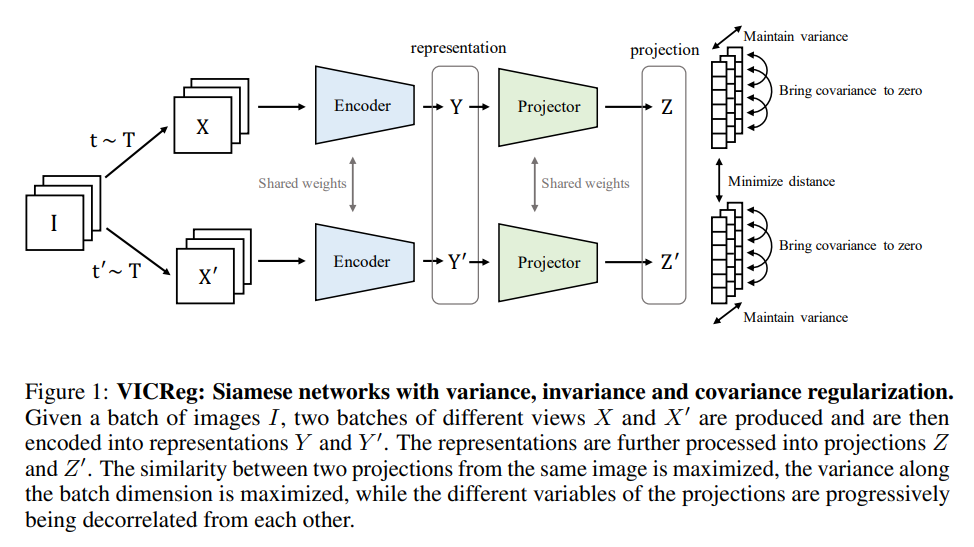
Variance

The variance regularization term is given by a [[hinge-loss]]:

$v(Z) = \frac{1}{d}\sum_{j=1}^{d}\max(0, \gamma - \sqrt{\mathrm{Var}(Z_{:,j}) + \epsilon})$

where $\gamma$ is a target value for the standard deviation (fixed to one for this paper)², and $\mathrm{Var}(x)$ is the variance estimator:

$\mathrm{Var}(x) = \frac{1}{n - 1}\sum_{i=1}^n(x_i - \bar{x})^2$

This forces the variance in a batch of embeddings to be $\gamma$ along each dimension.

Covariance

The covariance of matrix $Z$ is given as:

$C(Z) = \frac{1}{n - 1}\sum_{i=1}^n(Z_i - \bar{Z})(Z_i - \bar{Z})^T$

with $\bar{Z}$ being the mean embedding across a batch. The actual covariance loss term is taken as the squared off-diagonal coefficients of $C$ that scales with dimensionality $1/d$:

$c(Z) = \frac{1}{d}\sum_{i\neq j}C(Z)^2_{i,j}$

So that we force the embeddings to learn unit Gaussians similar to the $\beta$-regularization in [[variational autoencoder]].

Invariance

The invariance loss is given by:

$s(Z,Z') = \frac{1}{n}\sum_i \vert\vert Z_i - Z'_i \vert\vert ^2_2$

i.e. the mean squared Euclidean distance between each network embedding pair.

• This encourages the model to learn the same upstream representation for nominally the same input.

The full loss

$l(Z,Z') = \lambda s(Z,Z') + \mu\{v(Z) + v(Z')\} + v\{c(Z) + c(Z')\}$

with hyperparameters $\lambda$, $\mu$, and $\nu$.

Comments

[variational autoencoder]: variational autoencoder "variational autoencoder"